Details
A major objective in a conduction analysis is to determine the temperature field in a medium resulting from conditions imposed on its boundaries. That is, it is desired to know the temperature distribution, which represents how temperature varies with position in a medium. Once this distribution is known, the conduction heat flux at any point in the medium or on its surface may be computed from Fourier's law. Other important quantities of interest may also be determined. For a solid, knowledge of the temperature distribution could be used to ascertain structural integrity through determination of thermal stresses, expansions, and deflections. The temperature distribution could also be used to optimize the thickness of an insulating material or to determine the compatibility of special coatings or adhesives used with the material.
The manner in which the temperature distribution can be determined is considered: The approach follows the methodology described in the application of the energy conservation requirement. In this case, a differential control volume is defined, the relevant energy transfer processes are identified, and the appropriate rate equations are introduced. The result is a differential equation whose solution, for prescribed boundary conditions, provides the temperature distribution in the medium.
Cartesian Coordinates
Consider a homogeneous medium within which there is no bulk motion (advection) and the temperature distribution T(x, y, z) is expressed in Cartesian coordinates. Following the methodology of applying conservation of energy, an infinitesimally small (differential) control volume, dx ⋅ dy ⋅ dz is first defined and shown. Choosing to formulate the first law at an instant of time, the second step is to consider the energy processes that are relevant to this control volume. If there are temperature gradients, conduction heat transfer will occur across each of the control surfaces. The conduction heat rates perpendicular to each of the control surfaces at the x, y, and z coordinate locations are indicated by the terms qx, qy, and qz, respectively. The conduction heat rates at the opposite surfaces can then be expressed as a Taylor series expansion where, neglecting higher order terms:
The first equation for example, states that the x component of the heat transfer rate at x + dx is equal to the value of this component at x plus the amount by which it changes with respect to x times dx.
Within the medium there may also be an energy source term associated with the rate of thermal energy generation. This term is represented as:
(Eq2) 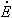 g =
g = 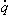 dx dy dz
dx dy dz
where 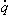 is the rate at which energy is generated per unit volume of the medium (W/m3). In addition, changes may occur in the amount of the internal thermal energy stored by the material in the control volume. If the material is not experiencing a change in phase, latent energy effects are not pertinent, and the energy storage term may be expressed as:
is the rate at which energy is generated per unit volume of the medium (W/m3). In addition, changes may occur in the amount of the internal thermal energy stored by the material in the control volume. If the material is not experiencing a change in phase, latent energy effects are not pertinent, and the energy storage term may be expressed as:
| (Eq3) | 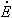 st = ρ cp st = ρ cp | | dx dy dz |
|
where ρ cp ∂T/∂t is the time rate of change of the sensible (thermal) energy of the medium per unit volume.
Once again it is important to note that the terms 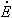 g and
g and 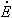 st represent different physical processes. The energy generation term
st represent different physical processes. The energy generation term 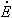 g is a manifestation of some energy conversion process involving thermal energy on one hand and some other form of energy, such as chemical, electrical, or nuclear, on the other. The term is positive (a source) if thermal energy is being generated in the material at the expense of some other energy form; it is negative (a sink) if thermal energy is being consumed. In contrast, the energy storage term
g is a manifestation of some energy conversion process involving thermal energy on one hand and some other form of energy, such as chemical, electrical, or nuclear, on the other. The term is positive (a source) if thermal energy is being generated in the material at the expense of some other energy form; it is negative (a sink) if thermal energy is being consumed. In contrast, the energy storage term 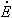 st refers to the rate of change of thermal energy stored by the matter.
st refers to the rate of change of thermal energy stored by the matter.
Conservation of energy must be expressed using the previous rate equations. On a rate basis, the general form of the conservation of energy requirement is:
Hence, recognizing that the conduction rates constitute the energy inflow, 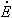 in, and outflow,
in, and outflow, 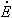 out, and substituting Eq2 and Eq3, the following is:
out, and substituting Eq2 and Eq3, the following is:
| (Eq5) | qx + qy + qz + 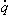 dx dy dz − qx+dx − qy+dy − qz+dz = ρ cp dx dy dz − qx+dx − qy+dy − qz+dz = ρ cp | | dx dy dz |
|
Substituting from Eq1a, Eq1b, and Eq1c, it follows that:
| (Eq6) | | – |
|
dx – |
|
dy – |
|
dz + |
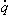 dx dy dz = ρ cp dx dy dz = ρ cp |
|
dx dy dz |
|
The conduction heat rates may be evaluated from Fourier's law:
where each heat flux component of Eq6a, Eq6b, and Eq6c from the lesson Fourier's Law, The Conduction Rate Equation, has been multiplied by the appropriate control surface (differential) area to obtain the heat transfer rate. Substituting Eq7a, Eq7b, and Eq7c into Eq6 and dividing out the dimensions of the control volume (dx dy dz), the following is obtained:
| (Eq8) |
|
( | k |
|
) | + | |
( | k |
|
) | + | |
( | k |
|
) | + |
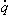 = ρ cp = ρ cp |
|
|
Eq8 is the general form, in Cartesian coordinates, of the heat diffusion equation. This equation, often referred to as the heat equation, provides the basic tool for heat conduction analysis. From its solution, the temperature distribution T(x, y, z) can be obtained as a function of time. The apparent complexity of this expression should not obscure the fact that it describes an important physical condition, that is, conservation of energy. The term ∂(k∂T/∂x)/∂x is related to the net conduction heat flux into the control volume for the x-coordinate direction. That is, multiplying by dx:
with similar expressions applying for the fluxes in the y and z directions. In words, the heat equation, Eq8, therefore states that at any point in the medium the net rate of energy transfer by conduction into a unit volume plus the volumetric rate of thermal energy generation must equal the rate of change of thermal energy stored within the volume.
It is often possible to work with simplified versions of Eq8. For example, if the thermal conductivity is constant, the heat equation is:
| (Eq10) | | + | |
+ | | + | 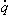 | | k |
| = | | |
|
where α = k/ρcp is the thermal diffusivity. Additional simplifications of the general form of the heat equation are often possible. For example, under steady-state conditions, there can be no change in the amount of energy storage; hence Eq8 reduces to:
| (Eq11) |
|
( | k |
|
) | + | |
( | k |
|
) | + | |
( | k |
|
) | + |
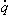 = 0 = 0 |
|
Moreover, if the heat transfer is one-dimensional (e.g., in the x direction) and there is no energy generation, Eq11 reduces to:
The implication of this result is that under steady-state, one-dimensional conditions with no energy generation, the heat flux is a constant in the direction of transfer (dq"x/dx = 0).
The heat equation may also be expressed in cylindrical and spherical coordinates. The differential control volumes for these two coordinate systems are shown in Fig2 and Fig3.
Cylindrical Coordinates
When the del operator ∇ of Eq3 from the lesson Fourier's Law, The Conduction Rate Equation is expressed in cylindrical coordinates, the general form of the heat flux vector, and hence of Fourier's law, is:
where:
are heat flux components in the radial, circumferential, and axial directions, respectfully. Applying an energy balance to the differential control volume of Fig2, the following general form of the heat equation is obtained:
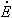 st = ρ cp
st = ρ cp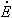 g =
g = 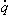 dx dy dz
dx dy dz
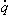 is the rate at which energy is generated per unit volume of the medium (W/m3). In addition, changes may occur in the amount of the internal thermal energy stored by the material in the control volume. If the material is not experiencing a change in phase, latent energy effects are not pertinent, and the energy storage term may be expressed as:
is the rate at which energy is generated per unit volume of the medium (W/m3). In addition, changes may occur in the amount of the internal thermal energy stored by the material in the control volume. If the material is not experiencing a change in phase, latent energy effects are not pertinent, and the energy storage term may be expressed as:
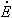 g and
g and 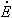 st represent different physical processes. The energy generation term
st represent different physical processes. The energy generation term 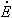 g is a manifestation of some energy conversion process involving thermal energy on one hand and some other form of energy, such as chemical, electrical, or nuclear, on the other. The term is positive (a source) if thermal energy is being generated in the material at the expense of some other energy form; it is negative (a sink) if thermal energy is being consumed. In contrast, the energy storage term
g is a manifestation of some energy conversion process involving thermal energy on one hand and some other form of energy, such as chemical, electrical, or nuclear, on the other. The term is positive (a source) if thermal energy is being generated in the material at the expense of some other energy form; it is negative (a sink) if thermal energy is being consumed. In contrast, the energy storage term 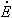 st refers to the rate of change of thermal energy stored by the matter.
st refers to the rate of change of thermal energy stored by the matter.
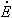 in +
in + 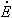 g −
g − 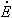 out =
out = 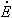 st
st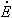 in, and outflow,
in, and outflow, 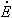 out, and substituting Eq2 and Eq3, the following is:
out, and substituting Eq2 and Eq3, the following is: