Quick
Normal strain is equal to deformation over original length. Normal strain is sometimes referred to as just strain, even though there are other types of strain such as shearing strain.
Equation
Nomenclature
Details
Normal strain indicates strain due to a normal force. This is probably the most basic type of strain that will be encountered. It can be defined as the deformation per unit length. Normal strain may be explained in terms of a rod subjected to axial loading.
A cylindrical rod of length L and uniform cross-sectional area A is fixed at one end. If a load P is applied to the free end of the rod, it elongates. The elongation is abbreviated by the symbol δ. A load-deformation diagram can be obtained by applying different loads and getting different lengths of deformation. But this information is only applicable for a rod of the same material and dimensions.
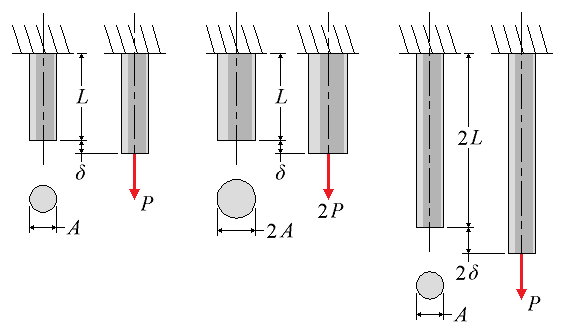
There are some relations that can make this information more applicable to fit parts with the same material but with different areas and different lengths. If a deformation δ is produced in the rod by a load P, then a load of 2P is required to cause the same deformation in a rod of the same length L, but of cross-sectional area 2A. This is because the stress is the same (P/A = 2P/2A). The load is proportional to the area. Also, a load P applied to a different rod, of the same cross-sectional area A, but of length 2L, causes a deformation 2δ in the rod. The length is proportional to the deformation. So, notice that in all cases the ratio of the deformation over the length of the rod is the same; it is equal to δ/L. This is strain, the ratio of deformation over the original length:
Normal strain expressed in this way is also a form of engineering strain. Further, if a part under consideration does not have a uniform cross-sectional area throughout, the stress will not be the same through the length of the part. Therefore, the strain is defined at a given point Q by considering a small element of undeformed length Δx. Denoting by Δδ the deformation of the element under the given loading, the normal strain at point Q is defined as:
Think about it this way, the strain is dependend on the load and the cross sectional area, which is the stress. Force over area is stress. If a part is under load, it will experience a certain elongation. If the part is made thinner and it is kept under the same load, it only makes sense that it will stretch more, it will have greater elongation. So the elongation is dependent on the force and area, or stress. That is why stress is mentioned. And the above equation takes into account a part that may have varying cross-sectional area. For more information about how force, cross-sectional area, and stress are related to strain, click here.
Related
▪ L - Deformation Due To Axial Loading
▪ L - Poisson's Ratio
