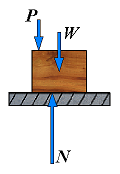
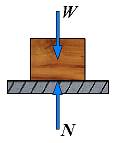
(Px = 0)
N = P + W
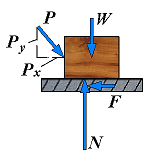
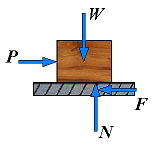
(Px < Fm)
F < μsN
N = Py + W
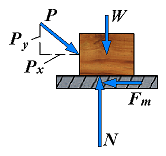
(Px = Fm)
Fm = μsN
N = Py + W
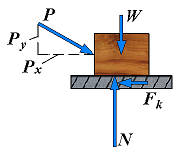
(Px > Fm)
Fk = μkN
N = Py + W
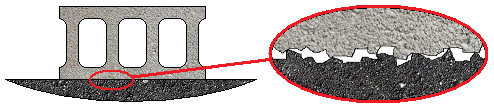
| Laws of Dry Friction and Coefficients of Friction |
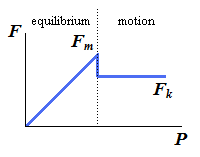
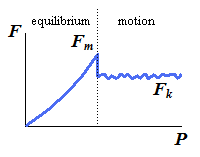
| Magnitude of the maximum static friction force | ||
| Magnitude of the kinetic friction force |
| symbol | description |
| Fm | maximum force |
| Fk | kinetic friction force |
| μs | coefficient of static friction |
| μk | coefficient of kinetic friction |
| N | normal component of the reaction surface |
| (Eq1) |
|
| (Eq2) |
|
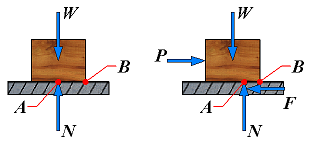
| 1. | No friction (Px = 0) | F = 0 N = P + W |  | The forces applied to the body do not tend to move it along the surface of contact; there is not friction force. |
| 2. | No motion (Px < Fm) | F = Px F < μsN N = Py + W |  | The applied forces tend to move the body along the surface of contact but are not large enough to set it in motion. The friction force F which has developed can be found by solving the equations of equilibrium for the body. Since there is no evidence that F has reached its maximum value, the equation Fm = μsN cannot be used to determine the friction force. |
| 3. | Motion impending (Px = Fm) | Fm = Px Fm = μsN N = Py + W |  | The applied forces are such that the body is just about to slide, that is, motion is impending. The friction force F has reached its maximum value Fm and, together with the normal force N, balances the applied forces. Both the equations of equilibrium and the equation Fm = μsN can be used. Also note that the friction force has a sense opposite to the sense of impending motion. |
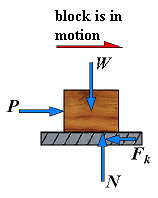
| 4. | Motion (Px > Fm) | Fk < Px Fk = μkN N = Py + W |  | The body is sliding under the action of the applied forces, and the equations of equilibrium do not apply any more. However, F is now equal to Fk and the equation Fk = μkN may be used. The sense of Fk is opposite to the sense of motion. |
| Next Lesson: Angles of Friction⇒ |