---

Entropy Generation

---

Details

The entropy change for an irreversible process is larger than the change in a reversible process for the same δQ and T. This can be written out in a common form as an equality:

(Eq1)

dS =   δQ T  + δSgen

provided the last term is positive:

(Eq2)

δSgen ≥ 0

The amount of entropy, δS_gen, is the entropy generation in the process due to irreversibilities occurring inside the system, a control mass for now but later extended to the more general control volume. This internal generation can be caused by process such as friction, unrestrained expansions, and the internal transfer of energy (redistribution) over a finite temperature difference. In addition to this internal entropy generation, external irreversibilities are possible by heat transfer over finite temperature differences as the δQ is transferred from a reservoir or by the mechanical transfer of work.

Eq2 is then valid with the equal sign for a reversible process and the greater sign for an irreversible process. Since the entropy generation is always positive and the smallest in a reversible process, namely zero, we may deduce some limits for the heat transfer and work terms.

Consider a reversible process, for which the entropy generation is zero, and the heat transfer and work terms therefore are:

δQ = T dS

and:

δW = P dV

For an irreversible process with a nonzero entropy generation, the heat transfer from Eq1 becomes:

δQ_irr = T dS − T δS_gen

and thus is smaller than that for the reversible case for the same change of state, dS. It is also noted that for the irreversible process, the work is no longer equal to P dV but is smaller. Furthermore, since the first law is:

δQ_irr = dU − δW_irr

and the property relation is valid:

T dS = dU + P dV

it is found that:

(Eq3)

δWirr = P dV − T δSgen

showing that the work is reduced by an amount proportional to the entropy generation. For this reason the term T δS_gen is often called "lost work," although it is not a real work or energy quantity lost but rather a lost opportunity to extract work.

Eq1 can be integrated between initial and final states to:

(Eq4)

S2 − S1 =   ∫  2    1  dS  =   ∫  2    1 δQ T   + 1S2 gen

Thus, an expression is obtained for the change of entropy for an irreversible process as an equality. In the limit of a reversible process, with a zero-entropy generation, the change in S expressed in Eq4 becomes identical to Eq1 in the lesson Entropy Change of a Control Mass During and Irreversible Process as the equal sign applies and the work term becomes ∫P dV. Eq4 is now the entropy balance equation for a control mass in the same form as the energy equation in Eq3 of the lesson First Law of Thermodynamics for a Change in State of a Control Mass, and it could include several subsystems. The equation can also be written in the general form:

Δ Entropy = + in − out + gen

expressing that entropy can be generated but not destroyed. This is in contrast to energy which can neither be created nor destroyed.

Some important conclusions can be drawn from Eq1 through Eq4. First, there are two ways in which the entropy of a system can be increased—by transferring heat to it and by having an irreversible process. Since the entropy generation cannot be less than zero, there is only one way in which the entropy of a system can be decreased, and that is to transfer heat from the system. These changes are illustrated in the following T-s diagram showing the halfplane into which the state moves due to a heat transfer or an entropy generation.


Fig1 - Change of entropy due to heat transfer and entropy generation.

Second, as it has been already noted for an adiabatic process, δQ = 0, and therefore the increase in entropy is always associated with the irreversibilities.

Finally, the presence of irreversibilities will cause the work to be smaller than the reversible work. This means less work out in an expansion process and more work into the control mass (δW < 0) in a compression process.

One other point concerning the representation of irreversible processes on P-V and T-S diagrams should be made. The work for an irreversible process is not equal to ∫P dV, and the heat transfer is not equal to ∫T dS. Therefore, the area underneath the path does not represent work and heat on the P-V and T-S diagrams, respectively. In fact, in many situations it is not certain of the exact state through which a system passes when it undergoes an irreversible process. For this reason it is advantageous to show irreversible processes as dashed lines and reversible processes as solid lines. Thus, the area underneath the dashed line will never represent work or heat. Fig2 shows an irreversible process, and, because the heat transfer and work for this process is zero, the area underneath the dashed line has no significance. Fig3 shows the reversible process, and area 1-2-3-4-1 represents the work on the P-V diagram and the heat transfer on the T-S diagram.

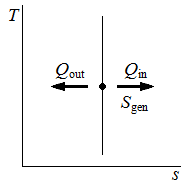
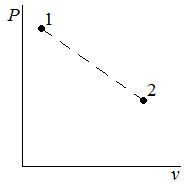
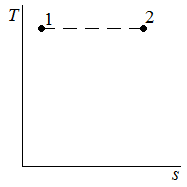
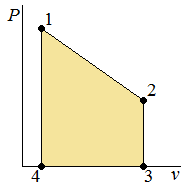
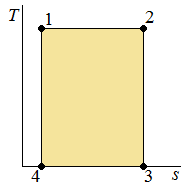
Fig2 - Irreversible process on a pressure-volume diagram.	Fig3 - Irreversible process on a temperature-entropy diagram.	Fig4 - Reversible process on a pressure-volume diagram.	Fig5 - Reversible process on a temperature-entropy diagram.