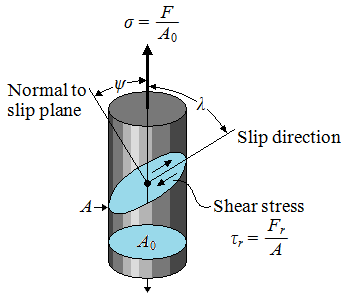
---

Schmid's Law

---

Quick
Schmid's law defines the relationship between shear stress, the applied stress, and the orientation of the slip system. It is an equation for finding the stress in the slip plane given an axial force and the angle of the slip plane. Schmid's law can help to explain the differences in behavior of different metals when subjected to a unidirectional force.


Equations

(Eq1)     τr = σ cos ψ cos λ

Schmid's Law

Nomenclature

F	unidirectional force
λ	angle defining slip direction relative to the force
ψ	angle defining the normal to the slip plane
Fr	shear force
A	area of slip plane
τr	resolved shear stress in the slip direction
σ	unidirectional stress applied to the cylinder

Details

The differences in behavior of metals that have different crystal structures can be understood by examining the force required to initiate the slip process. Suppose a unidirectional force F is applid to a cylinder of metal that is a single crystal as shown:

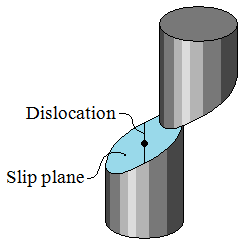
A resolved shear stress τ is produced on a slip system	Movement of dislocations on the slip system deforms the material

The slip plane and slip direction to the applied force can be oriented by defining the angles λ and ψ. λ is the angle between the slip direction and the applied force, and ψ is the angle between the normal to the slip plane and the applied force.

In order for the dislocation to move in its slip system, a shear force acting in the slip direction must be produced by the applied force. This resolved shear force F_r is given by:

F_r = F cos λ

If the equation is divided by the area of the slip plane, A = A₀/cos ψ, Schmid's law is obtained:

Eq1	τr = σ cos ψ cos λ

where:

τr =

Fr A

and:

σ =

F A0